Diffraction gratings are optical components that split a light source into multiple beams of colored light, which then move in different directions than the original beam of light, in a process called angular dispersion. Factors such as the light’s original wavelength, the spacing of the grating, and more can impact the dispersion and manipulation of light within the optical device that is utilizing the diffraction grating. In this article, we’ll explore this angular dispersion process, its formula, and its role in optical manufacturing.
What is Angular Dispersion?
White light is composed of all of the different colors of light (red, blue, ultraviolet, etc.) and is therefore considered polychromatic. Each color of light within a polychromatic beam of white light has its own associated wavelength range. These wavelengths are grouped into three ranges: ultraviolet, visible, and infrared.
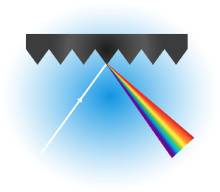
As polychromatic light enters or interacts with a prism or a diffraction grating, each color of light is separated out and spreads in a different direction. The goal of the grating is to disperse each color in a slightly different direction, or angle of dispersion, and isolate individual wavelengths of light. This separation of light is referred to as the process of angular dispersion.
Diffraction gratings enable optical devices, such as spectrometers, to utilize angular dispersion and isolate various wavelengths of light at different angles as they emerge, reflect, or refract off of the grating.
The Angular Dispersion Formula
To better understand angular dispersion, one can refer to the grating equation:
sin(angle of diffraction) = sin(angle of incidence) + order of diffraction*(light wavelength/grating period)
- Order of diffraction. The order of diffraction corresponds with how light is diffracted through the grating. For example, if the order of diffraction is +1, colors with increasing wavelengths are diffracted at increasing angles.
- Angle of incidence. When a ray of light hits a grating at a point, the angle of incidence is the angle between the incident ray and the normal. The normal refers to the line perpendicular to the grating at the point of incidence.
- Angle of diffraction. Light passing through a diffraction grating is diffracted in different directions. The angle of diffraction refers to the angle between each diffracted beam.
This equation gives the angle of diffraction for each order based on the given angle of incidence. The larger the grating period, or space between grooves, the more diffracted orders there are. The different variables in the equation control how the dispersed light appears.
For example, diffracted beams can have overlapping colors if the grating density is at the right level. Light at the higher end of the spectral order is also more likely to overlap. Finely controlling the grating allows manufacturers to control the spread and overlap of the different chromatic wavelengths of light.
Grating Blaze Wavelength and Groove Density
When it comes to angular dispersion from diffraction gratings, there are two important factors to consider: grating blaze wavelength and groove density.
Grating Blaze Wavelength
Blazing involves optimizing a grating for a particular wavelength; the blazing process requires a polished grating surface to be etched (or blazed) with a laser to create a series of microscopic indentations through the grating. These gratings control how each wavelength of polychromatic light is reflected, refracted, or transmitted. Every blazed optical component is built for a specific direction and angle of light — the blaze angle — at which it is most efficient. The steps, or groove facets, of the grating are tilted to a certain degree so that the diffracted and reflected light both transfer in the same direction.
Groove Density
Light dispersal can change depending on how many grooves are present on the diffraction grating; the count of grooves per unit of length is called groove density or groove frequency. This is usually universally expressed in grooves per millimeter, or g/mm. For example, a grating with 30 groves per 1 millimeter would be written as “30/1” or simply “30 groove density.” Manufacturers can control the depth, profile, and density of the etched grooves within a diffraction grating to control the colors and clarity of light. A change to any of these three critical factors – groove depth, profile/angle, and density – will affect the efficiency and strength of the light, the image’s resolution, and the total spectral range the device can transmit or reflect.
There is an inverse relationship between groove density and diffraction angles:
- Coarse gratings with low density (fewer grooves) have higher diffraction angles and orders
- Gratings with higher groove density (more grooves) have lower diffraction angles and orders
Gratings that are referred to as coarse have low density, or fewer grooves in the same amount of length. The amount of space between each groove results in higher diffraction orders and high diffraction. This means that smaller gratings can achieve more light diffraction with a small physical footprint in an optical device. Echelle gratings are an example of a coarse type of grating with low groove density and high angle of diffraction. This type of diffraction grating is a favorite for spectrographs and astronomical instruments.
Diffraction Gratings from OPCO Laboratory, Inc.
At OPCO Laboratory, Inc., we design and manufacture high-quality optical components that meet our customer’s needs for clear, refined light. We are ITAR-registered and can produce diffraction gratings that are powerful enough to be used in specialized applications for the defense, aerospace, medical, and semiconductor industries. To learn more about angular dispersion and diffraction gratings, contact us today for assistance from our optical experts